3.1.Ausgleichsergebnisse - Interpretation der Ergebnisse
Die Anzeige der Ausgleichungsergebnisse ermöglicht das Aufdecken grober Fehler mit Hilfe von statistischen Testgrößen für jede Messung. In der Tabelle befinden sich alle Beobachtungen, sortiert nach diesem Kriterium, große Werte zu oberst. Die betreffenden Beobachtungen können durch Doppelklick mit der linken Maustaste deaktiviert werden. Anschließend kann die Ausgleichung wiederholt werden, wobei nur mehr aktive Beobachtungen – durch einen roten Haken gekennzeichnet – berücksichtigt werden.
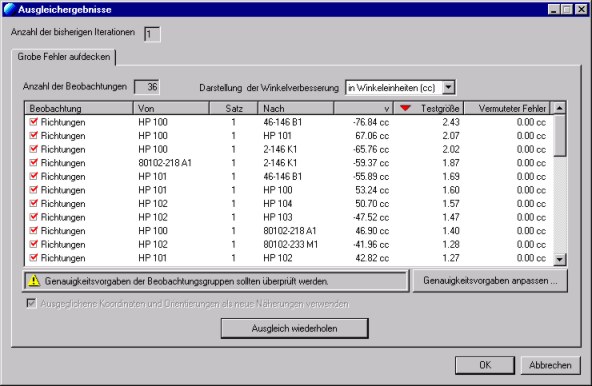
Satz
Falls durch entsprechende Einstellungen in den „Präprozessing Optionen“ Strecken oder trigonometrische Höhendifferenzen gemittelt werden ist das am Satz erkennbar. Vorne stehen die Hinmessungen, getrennt durch Komma. In Klammer stehen die Gegenmessungen, getrennt durch Komma.
Beispiel:
Von „A“, nach „B“, Satz „1,2 (3,4)“ bedeutet, dass diese Messung ein Mittel aus folgenden Messungen ist:
Von „A“ nach „B“, Satz 1
Von „A“ nach „B“, Satz 2
Von „B“ nach „A“, Satz 3
Von „B“ nach „A“, Satz 4
Statistische Tests:
Bei der Ermittlung und Verarbeitung großer Datenmengen muß stets auch mit dem Vorhandensein von groben Fehlern gerechnet werden (z.B. Ablesefehler, Punktverwechslungen, Registrierfehler,…). Es handelt sich dabei im statistischen Sinn um Modellfehler, die jeweils auf eine einzelne Beobachtung (Messung) beschränkt sind.
Ein Beobachtungsfehler in einer Messung wirkt sich grundsätzlich auf alle Verbesserungen aus und verfälscht den gesamten Fehlerhaushalt des Netzes. Der prozentuelle Anteil eines groben Fehlers, der sich in der dazugehörigen Verbesserung niederschlägt und damit nicht die Unbekannten verfälscht wird als Redundanzanteil r bezeichnet. Es ist also besser, nicht die Verbesserung auf grobe Fehler hin zu betrachten, sondern eine aus dieser abgeleitete standardisierte Testgröße. Als Grenzwert wird ein Fraktil einer statistischen Verteilung verwendet. Liegt die Testgröße unterhalb dieses Wertes (Nullhypothese), ist mit einer Wahrscheinlichkeit von 95% ein grober Fehler auszuschließen. Liegt die Testgröße jedoch über dieser Grenze, kann positiv auf das Vorhandensein eines Ausreißers geschlossen werden.
Die Berechnung der Testgrößen erfolgt durch Normierung der Verbesserung mit ihrer Standardabweichung.
Die Netzkonfiguration und das stochastische Modell sind darin integriert.
Data-Snooping wenn 5 oder weniger Überbestimmungen vorliegen, d.h. Freiheitsgrad<= 5
Testgröße…..![]()
Verglichen wird die errechnete Testgröße mit dem 95%-Fraktil aus der Normalverteilung
Multipler t-Test wenn mehr als 5 Überbestimmungen vorliegen, d.h. Freiheitsgrad > 5
Testgröße….. ![]()
Verglichen wird die errechnete Testgröße mit dem 95%-Fraktil aus der t – Verteilung
Empirische Zuverlässigkeit („vermuteter Fehler“): Da der Redundanzanteil r denjenigen Prozentsatz angibt, der bei einem groben Fehler in dieser Messung durch die Verbesserung „abgefangen“ also nicht „verschmiert“ wird, berechnet sich die vermutete Größe des Ausreißers (EZ) durch
Empirische Zuverlässigkeit ….. ![]()
Eine sinnvolle Interpretation dieses Wertes ergibt sich ausschließlich wenn in dieser Messung ein grober Fehler angezeigt wird.
Anmerkung: Die Aufdeckung von groben Fehlern erfolgt iterativ, da jeweils nur die Messung mit der betragsgrößten Testgröße ausgeschlossen werden darf.
Es besteht die Option, die ausgeglichenen Koordinaten und Orientierungen als nächste Näherung für eine neue Ausgleichung zu verwenden, oder die bestehenden Näherungen beizubehalten.
Die Darstellung der Winkelverbesserungen kann zur besseren Interpretierbarkeit wahlweise auch als Perpendikel (mm) im Zielpunkt erfolgen.
