Der Ansatz der Genauigkeiten der Messungen (stochastisches Modell) zu Beginn einer Netzausgleichung beruht meist auf Werksangaben der Gerätehersteller oder oft auf eigenen Erfahrungswerten. Will man die Genauigkeit einer Messgruppe aber aus den verwendeten Messanordnung statistisch abgesichert selbst schätzen, leistet die Varianzkomponentenschätzung gute Dienste. Dabei werden für jede Messgruppe aus der Ausgleichung Gruppengenauigkeiten ermittelt und im nächsten Iterationsschritt als stochastisches Modell verwendet.
Zwei Bedingungen sollten beim Einsatz der Varianzkomponentenschätzung stets erfüllt sein:
– die Beobachtungstypen oder –gruppen sollen in sich ausreichend überbestimmt und
– über die Messkonfiguration gut miteinander verknüpft sein
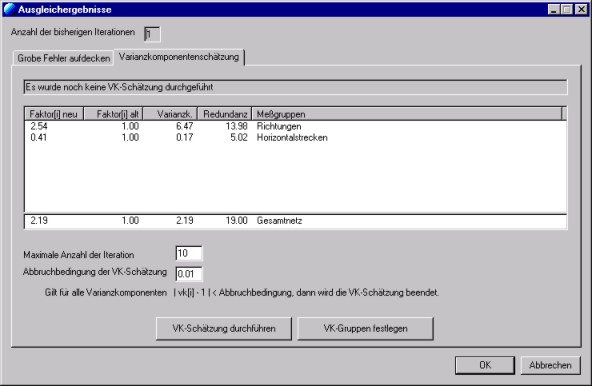
Das führt zu einer iterativen Verbesserung und nach mehreren Iterationsschritten wird das Verfahren konvergieren. Nach jeder Iteration entscheidet ein statistischer Test, ob das Iterationsziel erreicht ist. Ist dies der Fall, wird keine weitere Iteration gerechnet. Die max. Anzahl von Iterationen, die in einem Durchgang gerechnet werden, kann eingegeben werden. Nach Beendigung der Berechnung werden die a priori – und die a posteriori – Standardabweichungen aller Messgruppen gegenübergestellt.
Es bedeuten:
Faktor[i] neu …. Faktor für die Genauigkeit der Messgruppe nach der Varianzkomponentenschätzung
Faktor[i] alt …. Faktor für die Genauigkeit der Messgruppe vor der Varianzkomponentenschätzung
Varianzk. …………berechnete Varianzkomponente s2[0i] der Beobachtungsart oder -gruppe
Redundanz … Redundanzanteil (Kontrolliertheit) der entsprechenden Messgruppe durch andere Messgruppen
In der untersten Zeile der Tabelle wir die Werte für das Gesamtnetz angegeben, wobei hier unter Faktor alt der a priori-Wert für s20 und unter Varianzk. der Wert für das aus der Gesamtausgleichung berechnete s20 zu verstehen ist.